欧氏几何深度解析：11-14章攻略大全及学习指南

欧氏几何，作为数学的重要分支，对于培养学生的逻辑思维和空间想象力具有不可替代的作用。本文将围绕欧氏几何深度解析的第11至14章，为读者提供一份详尽的攻略大全及学习指南，帮助读者更好地掌握这一领域的核心知识，并引发对几何学的深厚兴趣。

欧氏几何是几何学的一个重要体系，主要研究平面和空间的性质。第11至14章是欧氏几何中的核心内容，涵盖了平面几何、立体几何以及相关的证明和应用。对于这一部分的深入学习，将有助于读者更好地理解空间结构，培养逻辑思维和推理能力。

三、攻略详解

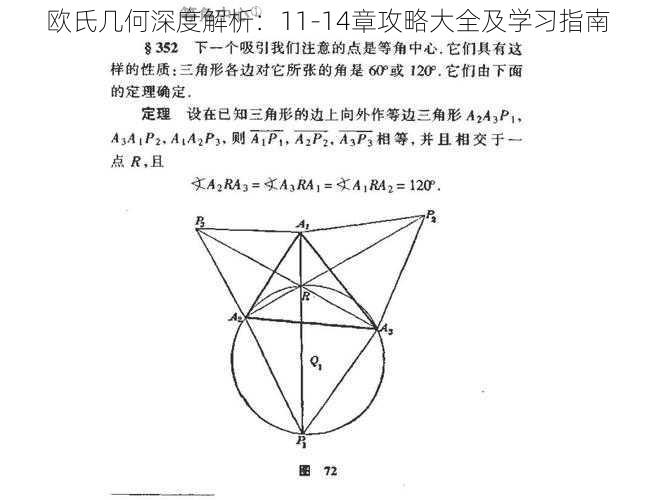
1. 平面几何的深入探究

角度与线段：本章主要探讨角度和线段的性质，如角的平分线、线段的中点等。通过学习这些性质，可以更好地理解平面图形的构造和性质。

相似与全等：相似图形和全等图形的概念是本章的重点。理解这些概念对于后续的立体几何学习有着重要作用。

应用实践：本章还会介绍一些与生活实际相结合的应用题，如建筑、绘图等，使读者能够将所学知识应用到实际生活中。

2. 立体几何的奥秘

空间图形的认识：学习如何从三维的视角理解空间图形，如点、线、面、体等。这是立体几何的基础。

体积与表面积：掌握计算立体图形的体积和表面积的方法，这是解决实际的基础。

空间关系：理解空间中的平行、垂直等关系，以及空间图形的位置关系，是立体几何的核心内容。

3. 几何证明的技巧与策略

直接证明法：通过已知条件和图形的性质，直接推导出结论的证明方法。

反证法：先假设结论不成立，然后通过推导得出矛盾，从而证明结论成立的方法。

构造法：通过构造特定的图形，利用图形的性质进行证明的方法。掌握这些证明技巧，对于解决复杂的几何具有重要意义。

4. 几何应用的实际场景

建筑与几何：建筑设计中广泛运用欧氏几何的原理，如建筑物的结构、布局等。

艺术与几何：艺术作品中，如绘画、雕塑等，也蕴含着丰富的几何元素。

日常生活中的应用：许多日常，如地图绘制、物品测量等，都可以通过欧氏几何的知识来解决。

四、总结及建议

通过对欧氏几何深度解析的第11至14章的学习，读者可以更加深入地理解平面和立体几何的性质、证明技巧以及实际应用。为了更好地掌握这部分内容，建议读者多做练习，培养空间想象力和逻辑思维能力。鼓励读者将所学知识应用到实际生活中，解决实际。未来的研究方向可以包括更深入的几何证明、与其他学科的交叉应用等。希望本文的攻略及指南能够帮助读者更好地学习欧氏几何，领略数学的魅力。